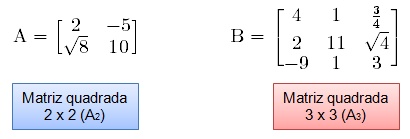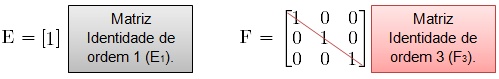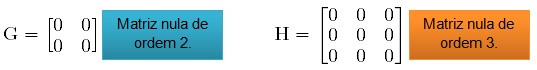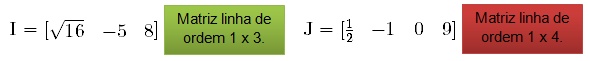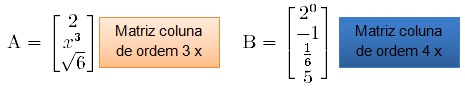2º ano

A análise combinatória é um dos tópicos que a matemática é dividida, responsável pelo estudo de critérios para a representação da quantidade de possibilidades de acontecer um agrupamento sem que seja preciso desenvolvê-los.

Veja um exemplo de um problema de análise combinatória e como montamos os seus agrupamentos.

Dado o conjunto B dos algarismos B = { 1,2,3,4}. Qual a quantidade de números naturais de 3 algarismos que podemos formar utilizando os elementos do grupo B?

Esse é um tipo de problema de análise combinatória, pois teremos que formar agrupamentos, nesse caso formar números de 3 algarismos, ou seja, formar agrupamentos com os elementos do conjunto B tomados de 3 em 3.

Veja como resolveríamos esse problema sem a utilização de critérios ou fórmulas que o estudo da análise combinatória pode nos fornecer.



Esse esquema construído acima representa todos os números naturais de 3 algarismos que podemos formar com os algarismos 1,2,3,4, portanto, concluindo que é possível formar 24 agrupamentos.

Para descobrir essa quantidade de agrupamentos possíveis não é necessário montar todo esse esquema, basta utilizar do estudo da análise combinatória que divide os agrupamentos em Arranjos simples, Combinações simples, Permutações simples e Permutações com elementos repetidos. Cada uma dessas divisões possui uma fórmula e uma maneira diferente de identificação, que iremos estudar nessa seção.

O estudo da análise combinatória é dividido em:

Princípio fundamental da contagem

Fatorial

Arranjos Simples

Permutação Simples

Combinação Simples

Permutação com elementos repetidos.

O determinante de uma Matriz é dado pelo valor numérico resultante da subtração entre o somatório do produto dos termos da diagonal principal e do somatório do produto dos termos da diagonal secundária. Nas matrizes quadradas de ordem 3x3 esses cálculos podem ser efetuados repetindo-se a 1ª e a 2ª coluna, aplicando em seguida a regra de Sarrus. Lembrando que uma matriz é quadrada quando o número de linhas é igual ao número de colunas. 
Observe o cálculo de determinantes nas seguintes matizes quadradas de ordem 2x2 e 3x3:

Determinante de uma matriz A de ordem 2 x 2.

Diagonal principal: 2 * 6 = 12
Diagonal secundária: 9 * (–1) = – 9

Det_A = 12 – (–9)
Det_A = 12 + 9
Det_A = 21 

Determinante de uma matriz B de ordem 3 x 3.

Regra de Sarrus

Diagonal principal 
2 * 6 * 3 = 36
5 * 7 * (–1) = – 35
6 * 1 * 2 = 12

Soma
36 + (–35) + 12
36 – 35 + 12
48 – 35 
13

Diagonal secundária
6 * 6 * (–1) = –36
2 * 7 * 2 = 28
5 * 1 * 3 = 15

Soma 
–36 + 28 + 15
–36 + 43
7

Det_B = 13 – 7 
Det_B = 6

Portanto, nas matrizes de ordem 2 x 2, calculamos o determinante de forma prática, multiplicando os elementos de cada diagonal e realizando a subtração do produto da diagonal principal do produto da diagonal secundária. Nas matrizes de ordem 3 x 3 utilizamos a regra de Sarrus descrita anteriormente.

Demonstração geral da Regra de Sarrus

Representando matrizes

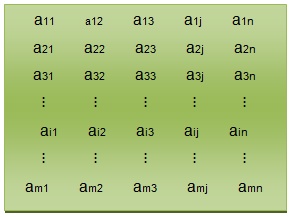
Uma matriz é, em geral, representa por uma letra maiúscula do nosso alfabeto (A, B, C, ...Z), enquanto os seus termos são representados pela mesma letra, desta vez minúscula, acompanhada de dois índices (a₁₁   a₁₂   a_{13 ...} a_mn), onde o primeiro representa a linha e o segundo a coluna em que o elemento está localizado.

Uma representação genérica de matriz é mostrada em seguida:

Chamemos esta matriz de A, e sua ordem é m x n, ou seja, m linhas e n colunas. Nela podemos observar o elemento a_ij, onde i representa a linha e j a coluna. Tomemos como exemplo o elemento a₃₂ → i = 3 e j = 2. O elemento está localizado na 3ª linha e na 2ª coluna. Ainda podemos chamar esta matriz de A = (a_ij)_{m x n.}

Tipos de matrizes

Matriz quadrada

Dizemos que uma matriz A de ordem m x n é quadrada, quando m = n. Isso significa que o número de linhas será igual ao número de colunas. Podemos representar este tipo de matriz por A_n.

Exemplos:

Matriz diagonal

A matriz, de ordem n (quadrada), diagonal é aquela em que todos os elementos acima e baixo da diagonal principal são nulos.

Matriz identidade

Matriz identidade é uma matriz quadrada de ordem n cujos elementos da diagonal principal são iguais a 1 e os elementos acima e abaixo desta diagonal são nulos (iguais a zero). Podemos representar esta matriz por I_n.

Matriz nula

Numa matriz nula, todos os elementos são iguais à zero. Podemos representar uma matriz nula m x n por 0_{m x n}; caso ela seja quadrada, indica-se por 0_n.

Matriz linha

É toda matriz que possui apenas uma linha. Numa matriz linha m x n, m = 1.

Matriz coluna

É toda matriz que possui apenas uma coluna. Numa matriz coluna m x n, n = 1.

• Matriz transposta: matriz A^t  obtida a partir da matriz A trocando-se ordenadamente as linhas por colunas ou as colunas por linhas. Por exemplo:

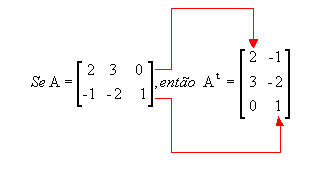
    Desse modo, se a matriz A é do tipo m x n, A^t é do tipo n x m.

   Note que a 1ª linha de A corresponde à 1ª coluna de A^t e a 2ª linha de A corresponde à 2ª coluna de A^t.

Igualdade de matrizes

   Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a mesma posição são iguais:

.

Operações envolvendo matrizes

Adição

   Dadas as matrizes , chamamos de soma dessas matrizes a matriz , tal que C_ij = a_ij + b_ij , para todo :

Exemplos:

Observação: A + B existe se, e somente se, A e B forem do mesmo tipo.

Propriedades

   Sendo A, B e C matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a adição:

a) comutativa: A + B = B + A

b) associativa: ( A + B) + C = A + ( B + C)

c) elemento neutro: A + 0 = 0 + A = A, sendo 0 a matriz nula m x n

d) elemento oposto: A + ( - A) = (-A) + A = 0

Subtração

   Dadas as matrizes , chamamos de diferença entre essas matrizes a soma de A com a matriz oposta de B:

Observe:

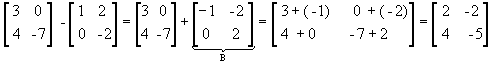
Multiplicação de um número real por uma matriz

   Dados um número real x e uma matriz A do tipo m x n, o produto de x por A é uma matriz B do tipo m x n obtida pela multiplicação de cada elemento de A por x, ou seja, b_ij = xa_ij:

    Observe o seguinte exemplo:

Propriedades

   Sendo A e B matrizes do mesmo tipo ( m x n) e x e y números reais quaisquer, valem as seguintes propriedades:

a) associativa: x . (yA) = (xy) . A

b) distributiva de um número real em relação à adição de matrizes: x . (A + B) = xA + xB

c) distributiva de uma matriz em relação à adição de dois números reais: (x + y) . A = xA + yA

d) elemento neutro : xA = A, para x=1, ou seja, A=A

Multiplicação de matrizes

   O produto de uma matriz por outra não é determinado por meio do produto dos sus respectivos elementos.

   Assim, o produto das matrizes A = ( a_ij) _{m x p}  e B = ( b_ij) _{p x n} é a matriz C = (c_ij) _{m x n} em que cada elemento c_ij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.

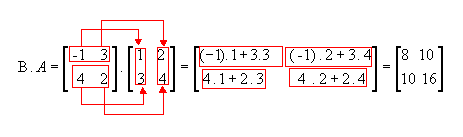
   Vamos multiplicar a matriz para entender como se obtém cada C_ij:

• 1ª linha e 1ª coluna

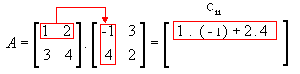
• 1ª linha e 2ª coluna

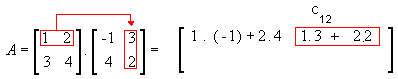
• 2ª linha e 1ª coluna

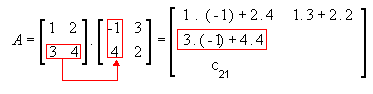
• 2ª linha e 2ª coluna

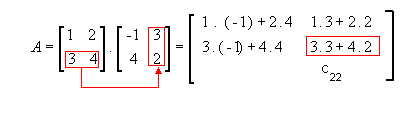
   Assim, .

   Observe que:

   Portanto, .A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.

   Vejamos outro exemplo com as matrizes :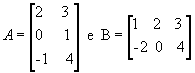

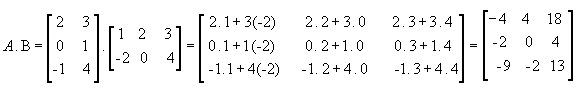
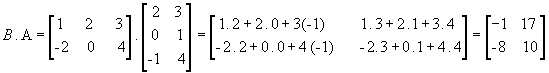
    Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número de linhas de B:

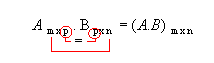
     A matriz produto terá o número de linhas de A (m) e o número de colunas de B(n):

• Se A_{3 x 2} e B _{2 x 5} , então ( A . B ) _{3 x 5}

• Se A _{4 x 1} e B _{2 x 3}, então não existe o produto

• Se A _{4 x 2} e B _{2 x 1}, então ( A . B ) _{4 x 1}