PORCENTAGEM
É frequente o uso de expressões que refletem acréscimos ou reduções em preços, números ou quantidades, sempre tomando por base 100 unidades. Alguns exemplos:
-
A gasolina teve um aumento de 15%
Significa que em cada R$100 houve um acréscimo de R$15,00 -
O cliente recebeu um desconto de 10% em todas as mercadorias.
Significa que em cada R$100 foi dado um desconto de R$10,00 -
Dos jogadores que jogam no Grêmio, 90% são craques.
Significa que em cada 100 jogadores que jogam no Grêmio, 90 são craques.
Razão centesimal
Toda a razão que tem para consequente o número 100 denomina-se razão centesimal. Alguns exemplos:
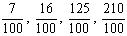
Podemos representar uma razão centesimal de outras formas:

As expressões 7%, 16% e 125% são chamadas taxas centesimais ou taxas percentuais.
Considere o seguinte problema:
João vendeu 50% dos seus 50 cavalos. Quantos cavalos ele vendeu?
Para solucionar esse problema devemos aplicar a taxa percentual (50%) sobre o total de cavalos.
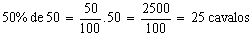
Logo, ele vendeu 25 cavalos, que representa a porcentagem procurada.
Portanto, chegamos a seguinte definição:
|
Porcentagem é o valor obtido ao aplicarmos uma taxa percentual a um determinado valor. |
Exemplos:
-
Calcular 10% de 300.
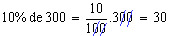
-
Calcular 25% de 200kg.
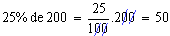
Logo, 50kg é o valor correspondente à porcentagem procurada.
Razão, Proporção e Porcentagem
Razão é uma forma de se realizar a comparação de duas grandezas, no entanto, para isto é necessário que as duas estejam na mesma unidade de medida.
A razão entre dois números a e b é obtida dividindo-se a por b. Obviamente b deve ser diferente de zero.
32 : 16 é um exemplo de razão cujo valor é 2, isto é, a razão de 32 para 16 é igual a 2.
Você só poderá obter a razão entre o comprimento de duas avenidas, se as duas medidas estiverem, por exemplo, em quilômetros, mas não poderá obtê-la caso uma das medidas esteja em metros e a outra em quilômetros ou qualquer outra unidade de medida que não seja o metro. Neste caso seria necessário que fosse eleita uma unidade de medida e se convertesse para ela, a grandeza que estivesse em desacordo.
Na razão, o número a é chamado de antecedente e o b tem o nome de consequente.
Porcentagem ou razão centesimal são as razões cujo termo consequente é igual a 100. Representamos a porcentagem através do símbolo "%".
10% é o mesmo que 0,10 (10 centésimos).
Proporção nada mais é que a igualdade entre razões.
Digamos que em determinada escola, na sala A temos três meninos para cada quatro meninas, ou seja, temos a razão de 3 para 4, cuja divisão de 3 por 4 é igual 0,75. Suponhamos que na sala B, tenhamos seis meninos para cada oito meninas, então a razão é 6 para 8, que também é igual 0,75. Neste caso a igualdade entre estas duas razões vem a ser o que chamamos de proporção, já que ambas as razões são iguais a 0,75.
Regra de três é um método de resolução de problemas que envolvem grandezas proporcionais.
"Um automóvel viajando a 80km faz determinado percurso em 2 horas. Se a viagem fosse realizada à velocidade de 120km, qual seria o tempo gasto?". Este é um exemplo de problema que pode ser resolvido via regra de três, no caso uma regra de três simples inversa.
A solução dos problemas de regra de três tem como base a utilização da "propriedade fundamental das proporções" e a "quarta proporcional".
Conjuntos
A Teoria dos conjuntos é a teoria matemática dedicada ao estudo da associação entre objetos com uma mesma propriedade, elaborada por volta do ano de 1872. Sua origem pode ser encontrada nos trabalhos do matemático russo Georg Cantor (1845-1918), os quais buscavam a mais primitiva e sintética definição de conjunto. Tal teoria ficou conhecida também como "teoria ingênua" ou "teoria intuitiva" por causa da descoberta de várias antinomias (ou paradoxos) associados à ideia central da própria teoria. Tais antinomias levaram a uma axiomatização das teorias matemáticas futuras, influenciando de modo indelével as ciências da matemática e da lógica. Mais tarde, a teoria original receberia complementos e aperfeiçoamentos no início do século XX por outros matemáticos.
O conhecimento prévio de tal teoria serve como base para o desenvolvimento de outros temas na matemática, como relações, funções, análise combinatória, probabilidade, etc.
Como definição intuitiva de conjuntos, dadas por Cantor, surgiam em sua teoria exemplos como:
- um conjunto unitário possui um único elemento
- dois conjuntos são iguais se possuem exatamente os mesmos elementos
- conjunto vazio é o conjunto que não possui nenhum elemento
- Os conjuntos podem ser finitos ou infinitos. Um conjunto finito pode ser definido reunindo todos os seus elementos separados por vírgulas. Já um conjunto infinito pode ser definido por uma propriedade que deve ser satisfeita por todos os seus membros.
A ideia de conjunto era um conceito primitivo e auto explicativo de acordo com a teoria; não necessitaria de definição.
Esta forma de representar um conjunto, pela enumeração de seus elementos é denominada "forma de listagem". Poderia-se representar o mesmo conjunto por uma determinada propriedade de seus elementos, sendo x, por exemplo, um número qualquer do conjunto Z representado abaixo:
Z = {1,3,5,7,9,11, ... }
teríamos, concluindo:
Z = { x | x é ímpar e positivo } = { 1,3,5, ... }.
Merece destaque outras relações básicas, que independem de um cálculo matemático mais complexo, utilizando-se lógica básica e pura. São exemplos desta afirmação as relações a seguir:
1 - Pertinência, que estabelece se um elemento pertence ou não pertence a um conjunto pré-estabelecido:
- dado um número x, caso ele pertença ao conjunto, escrevemos x ∈ A, ou "x" pertence ao conjunto A
- caso "x" não pertença ao conjunto, registra-se x ∉ A
- um conjunto sem elementos é um conjunto vazio, representado pela letra grega φ (phi)
2 - Subconjunto:
Caso todo o elemento do conjunto A pertença também ao conjunto B, sem que todos os elementos deste segundo grupo pertençam todos a B, diremos que "A é subconjunto de B": A ⊂ B
3 - Conjuntos numéricos fundamentais:
Trata-se de qualquer conjunto cujos elementos são números, entre eles, o conjunto de números naturais N = {0,1,2,3,4,5,6...}; o conjunto de números inteiros Z = {..., -4,-3,-2,-1,0,1,2,3,... } (sendo que N ⊂ Z); conjunto de números racionais Q = { 2/3, -3/7, 0,001, 0,75, 3, etc.) (sendo que N ⊂ Z ⊂ Q); conjunto de números irracionais, etc.
4 - União
Ocorre união quando o conjunto união contempla todos os elementos de dado conjunto A ou de dado conjunto B.
Exemplo: {0,1,3} ∪ { 3,4,5 } = { 0,1,3,4,5}
Assim, através de suas numerosas combinações, que fornecem poderosa ferramenta para a construção da matemática de base axiomática, apesar de seu conteúdo predominantemente dedutivo, logo surgiu o "Paradoxo de Russel", que é a contradição mais famosa da teoria dos conjuntos.
Conjunto dos Números Naturais
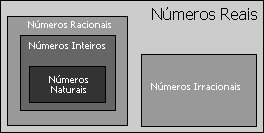
São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N.
Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar um * ao lado do N:
N = {0,1,2,3,4,5,6,7,8,9,10, ...}
N* = {1,2,3,4,5,6,7,8,9,10,11, ...}
Conjunto dos Números Inteiros
São todos os números que pertencem ao conjunto dos Naturais mais os seus respectivos opostos (negativos).
São representados pela letra Z:
Z = {... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
O conjunto dos inteiros possui alguns subconjuntos, eles são:
- Inteiros não negativos
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z+:
Z+ = {0,1,2,3,4,5,6, ...}
- Inteiros não positivos
São todos os números inteiros que não são positivos. É representado por Z-:
Z- = {..., -5, -4, -3, -2, -1, 0}
- Inteiros não negativos e não-nulos
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:
Z*+ = {1, 2, 3, 4, 5, 6, 7, ...}
Z*+ = N*
- Inteiros não positivos e não nulos
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.
Z*- = {... -4, -3, -2, -1}
Conjunto dos Números Racionais
Os números racionais é um conjunto que engloba os números inteiros (Z), números decimais finitos (por exemplo, 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da parte decimal infinitamente), como "12,050505...", são também conhecidas como dízimas periódicas.
Os racionais são representados pela letra Q.
Conjunto dos Números Irracionais
É formado pelos números decimais infinitos não-periódicos. Um bom exemplo de número irracional é o número PI (resultado da divisão do perímetro de uma circunferência pelo seu diâmetro), que vale 3,14159265 .... Atualmente, supercomputadores já conseguiram calcular bilhões de casas decimais para o PI.
Também são irracionais todas as raízes não exatas, como a raiz quadrada de 2 (1,4142135 ...)
Conjunto dos Números Reais
É formado por todos os conjuntos citados anteriormente (união do conjunto dos racionais com os irracionais).
Representado pela letra R.